1.
1-1. 직선의 기울기

2차원의 평면 위에서 기울기를 구하는 방법은 내가 알고 있듯이, X축 변화량과 Y축 변화량에 대해 계산하는 것.
그리고 극 값은 그 직선의 탄젠트 값과 같다.
1-2.

표현 방식을 기억해두자. 알고 있기는 하지만 낮설다.
1-3.

분자의 발산속도 < 분모의 발산속도 = 0에 수렴
분모의 발산속도 < 분자의 발산속도 = 무한으로 발산한다.
분자와 분보의 차수가 같을경우, 극한은 최고차항의 계수의 비와 같다.
1-4.

연속의 정의 = '함수의 그래프가 끊어지지 않고 이어져 있다'
끊어지지 않고 이어져 있다 = '함수값과 극한 값이 같다'
함수가 a에서 정의가 되지 않아도 극한 값은 존재할 수 있으며, 함수값과 극한값이 같지 않을 수도 있다.
이런 두 가지 경우 함수는 x= a에서 연속이 아니다.
연속 함수일 경우에는 극한 값과 함수 값은 같아야 한다.
첫 번째 그림의 경우, 함수의 함수(a)의 값은 c이며, 극한 값은 b다. 연속하지 않으므로 극한값과 함수값은 다르다.
두 번째 그림의 경우, 함수값은 c이며 좌극한 값은 b, 우극한 값은 c다.
좌극한 우극한의 값이 다르기 떄문에 극한은 없다.
극한 값이 존재하지 않기 때문에 불연속이다.
세 번째 그림의 경우, 극한값과 함수값이 같기 때문에 연속이다. 이를 아래와 같이 표현한다.

2.
2-1. 평균 변화율
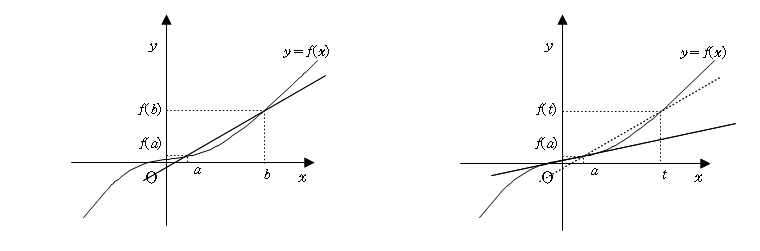
평균변화율이란 함수의 그래프 위의 두 점을 지나는 직선의 기울기다.
2-2. 미분계수의 계산
미분 = 함수의 접선의 기울기
이 말을 바꿔 말하면, 접선의 기울기는 b가 a에 한 없이 가까워 질 때의 평균변화율을 말한다

2-3. 접선(tangent line)의 방정식

공식으로 이해할 필요가 없다. 어떤 직선의 기울기와 지나는 점을 알고 있다면, 반드시 위의 식을 만족해야한다.
x1,과 y1이 해가 되어야 하고, 기울기가 m이여야 하니 말이다.

이 식을 어떤 함수에 대해서 적용시키면 위와 같다.
2-4. 법선의 방정식

법선이 왜 중요한 의미를 지니는 것일까? 90도이기 때문에?
기울기가 역수이기 때문에?
어떤 중요한 의미를 가지고 있는 것일까?
'2019년 혁신성장 청년인재 집중양성(빅데이터) > 수학 공부' 카테고리의 다른 글
| 미적분학의 기초(Introduction to Calculus) by 밝히리 4 (0) | 2019.08.02 |
|---|---|
| 미적분학의 기초(Introduction to Calculus) by 밝히리 3 (0) | 2019.08.02 |
| 미적분학의 기초(Introduction to Calculus) 1 (0) | 2019.07.29 |


