http://blog.daum.net/eigenvalue/3079253
[e-book] 미적분학의 기초
미적분학의 기초.hwp 2004년 9월 25일 새벽 2시 미적분학의 기초 올립니다. (카페 수학문제 푸는 동네에 처음 올림) 2004년 11월 18일 오후 6시 수정해서 올립니다. 내용 순서를 약간 바꾸었고 설명과 예제를 추가했습니다
blog.daum.net
미적분학과 선형대수에 대해 공부하기 위해 여러 자료를 보던 중, 밝히리님이 정리하신 자료를 찾았다.
그 노트를 보면서, 공부하고 다시 그 자료를 정리하려고 한다.
데이터 과학이라는 분야는 정말 만능을 요구하는 것 같다.
컴퓨터 언어를 다뤄야 하기에 언어적 센스도 필요하고
수학적 이론을 바탕으로 문제를 해결하기 위하여 수학도 어느정도 알아야 한다.
참 알아야 할 것이 많아서, 겁이 나기도 하지만
어쩔 수 있나, 필요하다면 공부 해야한다.
공부하면 할 수록 느끼는 것이지만
정말 몸고 생각은 변화하길 싫어하는 것 같다.
변할 수밖에 없는 것들이면서.
오늘도 하기 싫어서 미루다 미루다 지금 노트북을 켜고 자리에 앉았다.
시작이 반이라고 하니, 이 기초 공부도 끝이 나겠지.
다행히 밝히리라는 좋은 선생님을 만나서 다행이다.
미적분학의 기초를 정리 후엔
선형대수의 기초에 대해서 정리 할 것이다.
그 후에 확률과 통계에 대해서 정리를 할 예정이다.
8월 중으로 끝내고 싶지만, 가능할지는 모르겠다.
WAE4도 들어야 하기에...
1. 머리말
1-1.
1996년의 일이다. 내가 대학교 2학년 때 1학년 후배들을 가르친 적이 있었다. 그들에게
‘ y=x^2을 미분하면 뭐지?’ 라고 물으니
‘ 2x요.’라고 대답했다. 그래서 내가 다시
‘이 함수의 x=1 에서 접선의 기울기는 얼마지?’ 하고 물었더니 아무도 대답을 못했다. 고등학교에서 미적분을 배운 학생들이 이런 단순한 질문도 대답을 못하는 것에 나는 놀랐다. 지금도 가끔 미적분학을 고등학생들에게 가르치면, 그들은 도함수를 구하고 부정적분을 구하는 계산은 할 줄 안다. 그러나 미분이 의미하는 것이 무엇이고, 이 문제에서 왜 미분을 하며 왜 적분을 하는지, 그리고 미분과 적분 사이에는 어떠한 관계(미적분학의 기본정리를 뜻함)가 있는지를 제대로 알고 있는 사람이 별로 없었다.
나도 대답을 하지 못했다. 원체 수학이 약하기도 했지만, 못한다는 생각에 겁을 많이 먹고 공식만을 외웠었다.
수학 역시 세계를 해석하는 하나의 도구지만, 과거의 나에게는 시험 점수 그 이상의 의미는 없었던 것 같다.
2. 미분(differentiation)

2-1. 미분은 접선의 기울기다.
2-2. 접선의 기울기는 다른 말로 미분 계수(differntial coefficient) 혹은 순간변화율이라고 한다.
3. 도함수(derivative)

3-1. 도함수란 어떤 함수의 x의 각 값에 미분계수를 대응시키는 함수다. 즉 미분계수의 집합을 표현하는 함수가 도함수다.
3-2. 도함수를 구하는 것을 미분이라고 한다

3-3. 도함수의 도함수를 이계도함수라고 한다. 어떤 함수를 n번 미분한 함수를 n계 도함수라고 한다.
4. 함수의 그래프와 미분의 수학적 의미
4-1. 어떤 함수의 a에서의 미분계수가 0보다 크다면 그 함수는 a 근방에서 증가 상태에 있다.
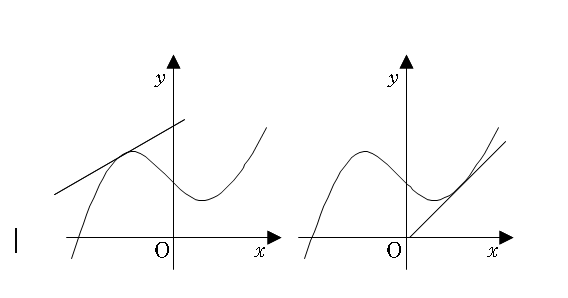
4-2. 어떤 함수의 a에서의 미분계수가 0보다 작다면 그 함수는 a 근방에서 감소 상태에 있다.
4-3. 일반적으로 어떤 함수는 a에서 증가상태에서 감소상태 혹은 반대로 바뀐다. 즉 극대값 또는 극소값을 갖는다. 예외도 있다. 그 경우 극값은 없다.
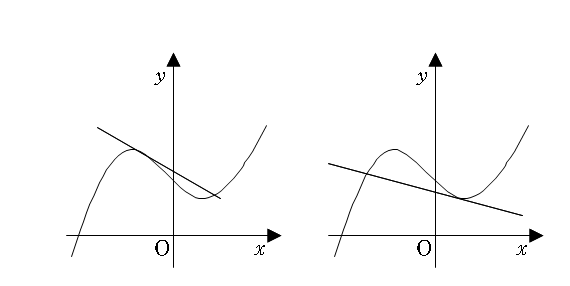
4-4. 어떤 함수의 이계도 함수가 0보다 크다면, 어떤 함수의 도함수는 a에서 증가상태이다. 즉, 어떤 함수는 a 근방에서 접선의 기울기가 커지고 있으므로, 아래로 볼록이다.
4-5. 어떤 함수의 이계도 함수가 0보다 작다면, 어떤 함수의 도함수는 a에서 감소상태이다. 즉, 어떤 함수는 a 근방에서 접선의 기울기가 작아지고 있으므로, 위로 볼록이다.
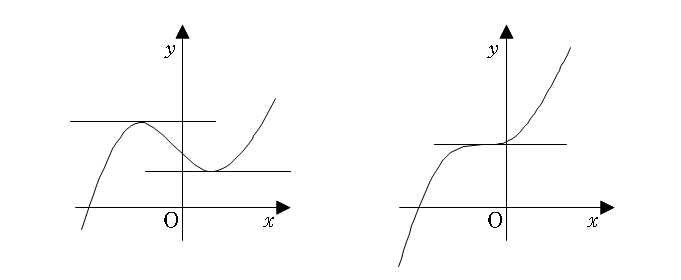
4-6. 어떤 함수의 이계도 함수가 0이면, 어떤 함수의 도함수는 a에서 극값을 갖는다. 즉, 어떤 함수는 a에서 변곡점을 가진다. 예외도 있다.
'2019년 혁신성장 청년인재 집중양성(빅데이터) > 수학 공부' 카테고리의 다른 글
| 미적분학의 기초(Introduction to Calculus) by 밝히리 4 (0) | 2019.08.02 |
|---|---|
| 미적분학의 기초(Introduction to Calculus) by 밝히리 3 (0) | 2019.08.02 |
| 미적분학의 기초(Introduction to Calculus) 2 by 밝히리 (0) | 2019.08.02 |


