A. K-Means Algorithms

1. 레이블이 없을 때, 사용되는 비지도학습 중 첫 번째인 K-Means Clsutering이다. 원리는 간단하다. 각 군집의 중심을 찾는 것이다. 다만 군집의 개수를 정해주어야 한다.

1. K-means algorithm은 간단하다. 첫 째, 몇 개의 클러스트를 만들지 정한다. K를 설정 한후, 임의의 중심 값을 설정한다.
2. 각 x는 가장 가까운 임의의 중심으로 할당 된다.
3. 군집으로부터 중심 값을 재설정한다.
4. 중심의 변화가 거의 없을 때까지 반복한다.
B. Optimization Objective
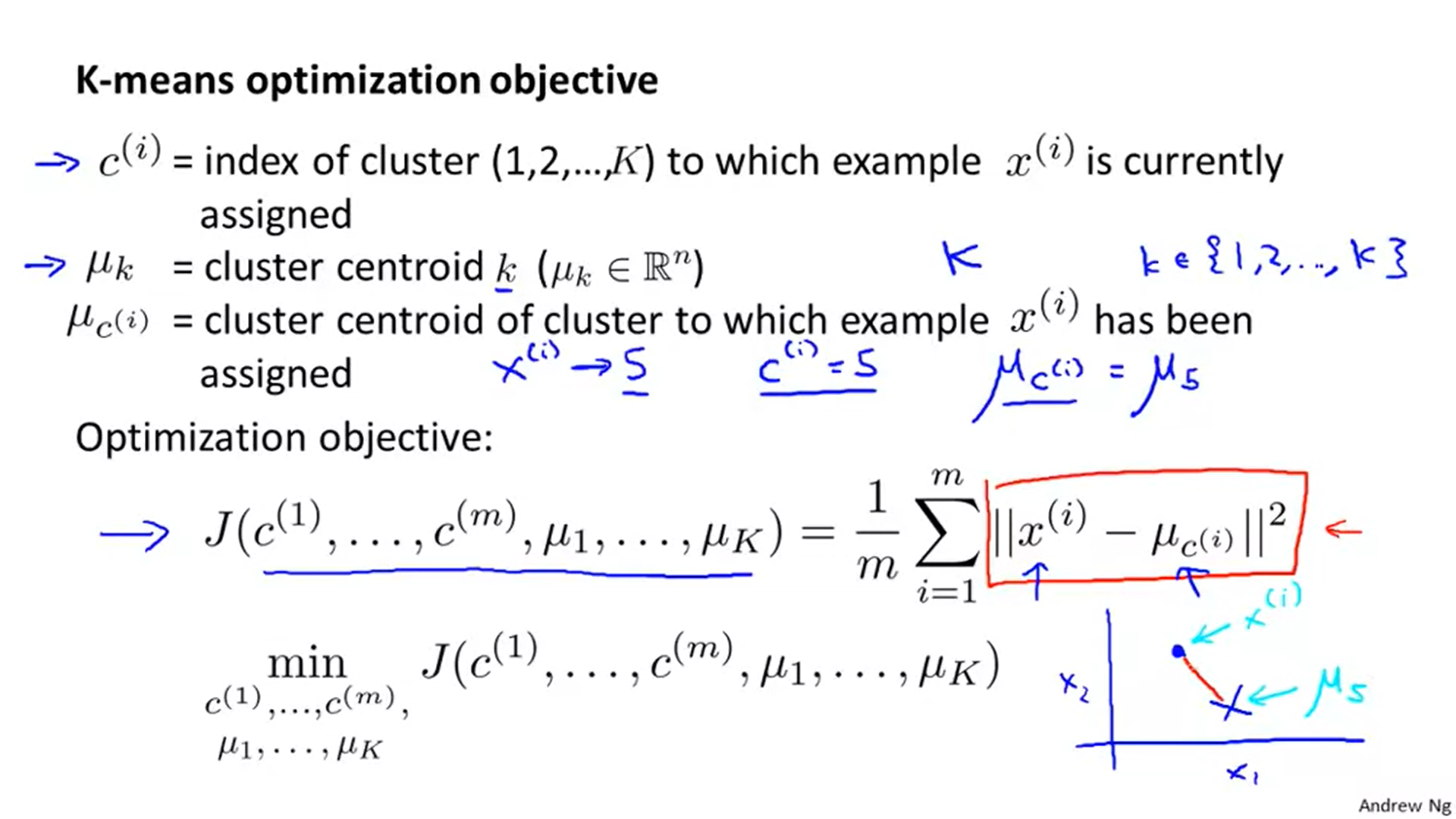
1. K-means algorithms의 최적화는 간단하다. 각 X의 할당된 중심 값으로 부터의 거리의 합이 최소가 되도록 하는 것이다.

2. 중심 값이 갱신 될 때마다, 이상적인 중심 값으로 다가가기 때문에, 반복 수가 증가할 수록, 비용(거리의 합)은 감소할 수밖에 없다.
C. Random Initialization
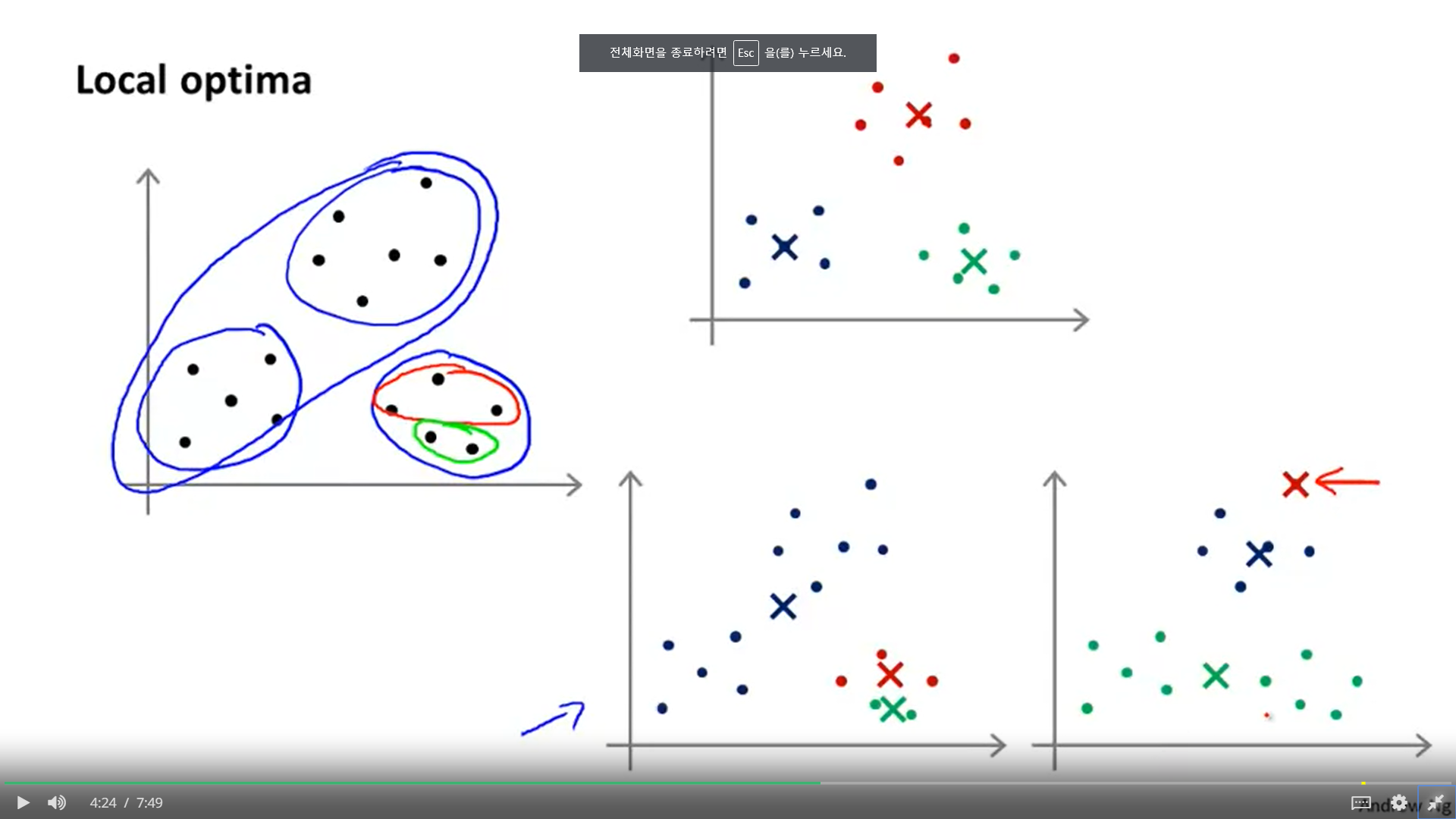
1, 어떻게 로컬 미니마를 피하냐?

1. 첫번 째, 임의로 선택을 하되, 우리가 가지고 있는 트레이닝 셋에서 임의로 뽑는다!
2. 둘 째, 한번 뽑지 말고 여러번 뽑아서 알고리즘을 돌린다.
3. 그 중 비용이 가장 적은 것을 뽑는다.
D. choosing the Number of Cluseters
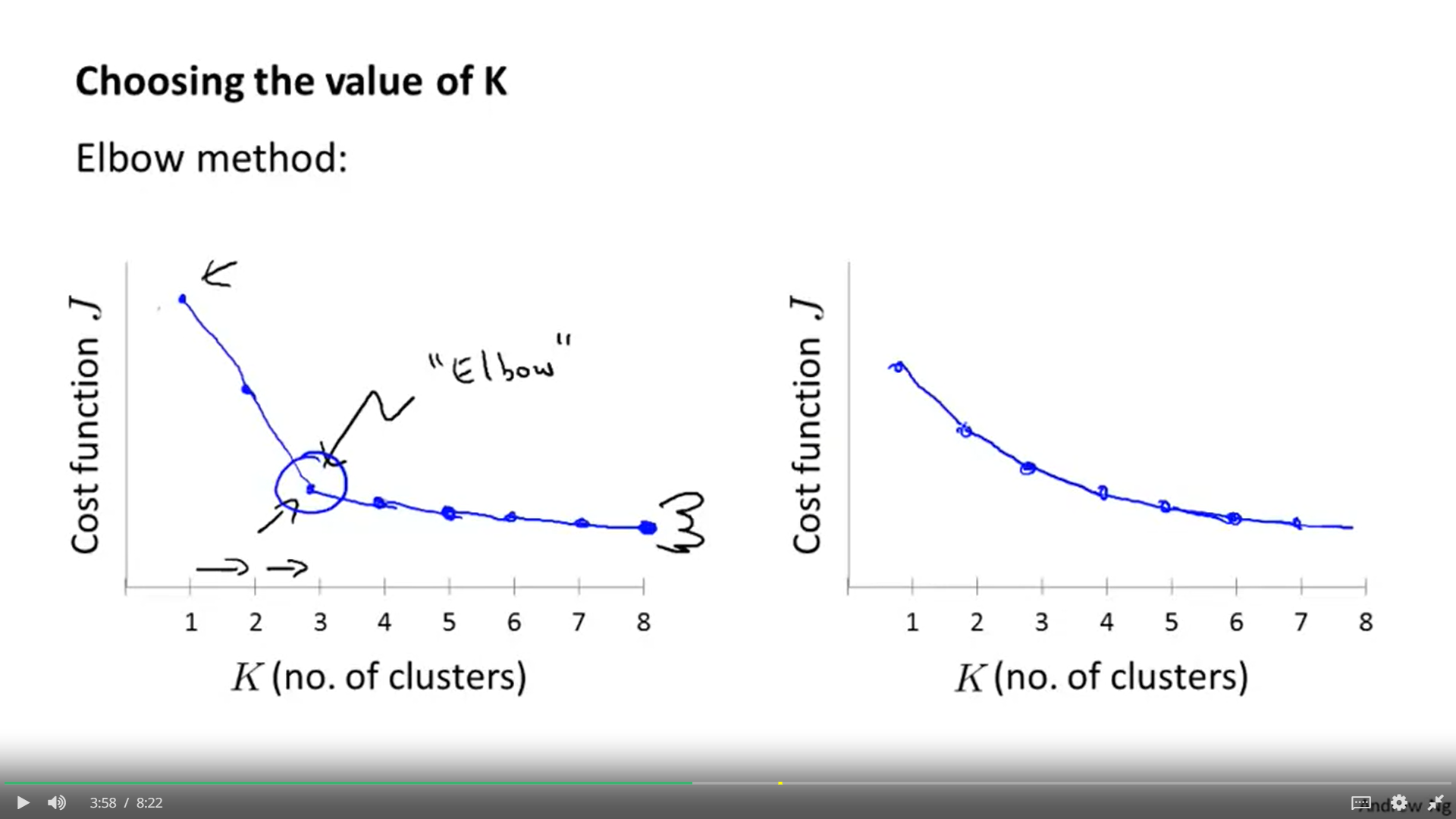
1. 어떻게 K를 정하냐? 첫 번째 방법이 Elbow method다. 비용함수가 급격히 감소하는 지점을 찾는 것이다.
2. 하지만 대부분의 경우 그 K를 찾는 것이 모호하다.
3. 이 K 값이 찾아지면, 여러번 알고리즘을 돌리면 된다.
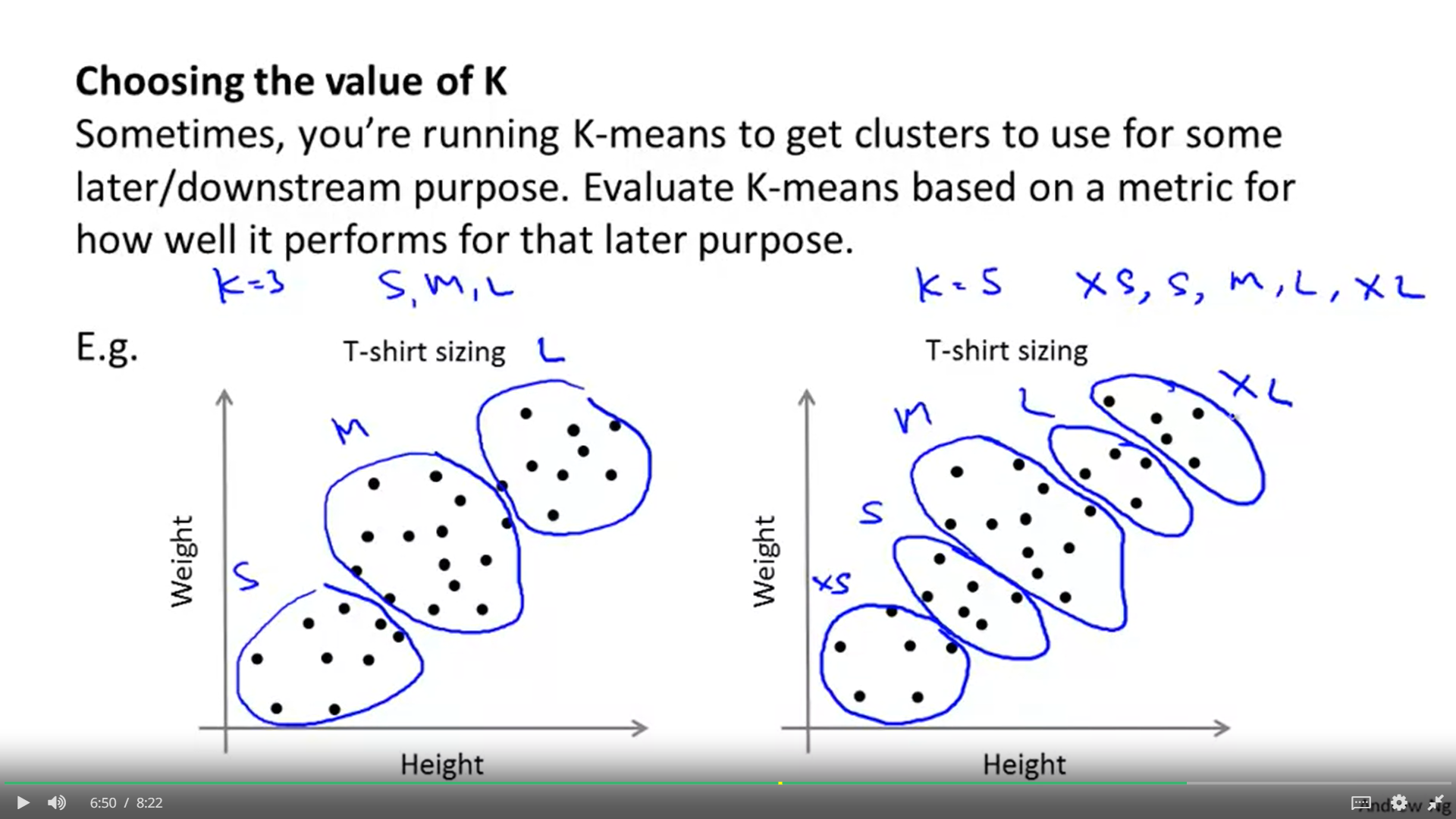
1. 티셔츠 사이즈를 결정하는 것처럼, 목적에 맞도록 K 값을 설정하는 편이 좋다.
2. 3사이즈로 파는 것이 좋다 혹은 다섯 사이즈로 파는 것이 좋다고 결정된다면 그 K값을 선택 한후 사이즈의 범위를 고르면 되는 것이다.
'2019년 혁신성장 청년인재 집중양성(빅데이터) > [COURSERA] Machine Learning Stanford Uni' 카테고리의 다른 글
| [week8] Principal Component Analysis (0) | 2019.11.03 |
|---|---|
| [week8] Data Compression (0) | 2019.11.03 |
| [week7] SVMs in Practice (0) | 2019.10.28 |
| [week7] Kernel (0) | 2019.10.28 |
| [Week7] Large Margin Classfication (0) | 2019.10.28 |



