A. Examples and Intuitions 1

https://ko.khanacademy.org/computing/computer-science/cryptography/ciphers/a/xor-bitwise-operation
XOR 비트 연산
ko.khanacademy.org
1. 먼저 배타적 논리합 (XOR)에대해서 짚고 넘어가야 한다. 배타적 논리합이란 하나만 참이고 하나는 거짓인 경우를 골라 내는 것인데, 그것을 하나의 연산으로만 구분할 수 없기 때문에 최소 2번 이상의 연산이 필요하다는 이야기다.
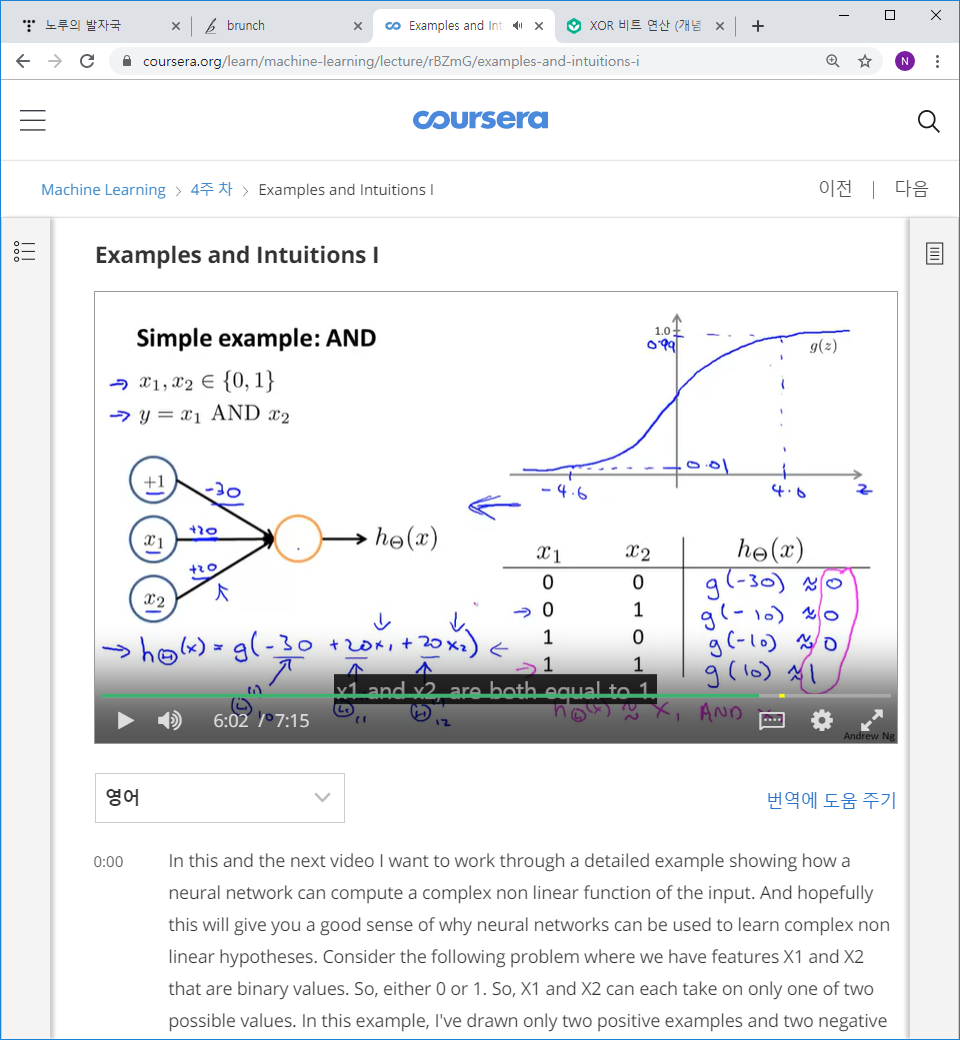
1. AND연산이라는 간단한 예제를 보면, X1과 ,X2의 값에 의해서 생긴 가설 H의 값이 X1과 X2가 모두 1일 일때만 1의 값을 가지는 것을 볼 수 있다. 이것이 AND연산이 되었음을 알려준다.

1. 이번에는 OR연산이다. 진리표를 그려보면 알 수 있듯이, 둘 중 하나만 1의 값을 가진다면, 가설 H는 1의 값을 가지게 된다.
2. 두 가지의 예가 하나의 뉴런이 할 수 있는 연산을 보여준다.
B. Examples and Intuitions 2

1. 세 번째 예시가 NEGATION(반대이다) 즉, X의 값이 0일 때, 가설은 1이라는 참의 값을 가지며, X의 값이 1일 때 H는 0이라는 부정 값을 가질 수 있게 된다. 반대 역시 하나의 뉴런으로 연산이 가능하다.
2. 또한 x1과 x2가 아닌 것들에 대해 분류를 할 때에도 마찬가지로, x1과 x2의 마이너스의 세타값음 줌으로써 구분을 할 수 있게 해준다.

1. AND연산으로 둘 값 모두 참인 곳에 대해서 연산을 할 수 있었지만, 값이 모두 참이고, 모두 거짓인 곳까지 한번에 걸를 수는 없었다. 즉 AND연산 한번을 통해, 모두 참이고, 모두 거짓인 곳에 대해서 질의 할 수 없었다는 말이다. 그 연산을 하기 위해서는 참을 거르는 AND연산과 거짓을 거리는 AND연산 그리고 OR연산이 필요하다.
2. 붉은 색으로 표시된 부분은 AND연산이고, 파랑색으로 표시된 부분은 거짓을 고르는 AND연산 초록색은 OR연산을 보여준다.
3. 진료표에서의 계산을 통해, 각 값이 레이어 2에서의 각 값이 0과 1로 구분되게 되고, 그 유닛을 or로 연산하여 우리가 원하는 둘 중 하나만 참인 논리를 연산할 수 있게 된다.
C. Multiclass Classification

1. 다양한 종류를 어떻게 분류할 것이가에 대해서는 One-vs-all 방법을 사용한다. 최대 우도법에 의해서 각 결과에서 최고 값을 가지는 것으로 분류를 하게 된다.

1. 아웃풋의 종류 만큼을 분류할 수 있게 되는 것이다.
'2019년 혁신성장 청년인재 집중양성(빅데이터) > [COURSERA] Machine Learning Stanford Uni' 카테고리의 다른 글
| [week6] Evaluating a Learning Algoritm (0) | 2019.10.06 |
|---|---|
| [week5] Neural Networks : Learning, Cost Function and Backpropagation (0) | 2019.10.03 |
| [week4] Neural Network (0) | 2019.09.30 |
| [week4] Non-linear Hypotheses, Motivation (0) | 2019.09.30 |
| [week3] Solving the Problem of Overfitting (0) | 2019.09.26 |



