
1. Underfitting = high bias, 과소적합은 강한 편향(bias), 강한 선입견(preconception)을 가지고 있다고 말할 수 있다. 데이터를 직선에 맞추려다보니 이러한 크 편향이 생겨버린 것이다.
2. 두 번째는 Overfitting 이라고 하면, 이를 high variance(높은 분산)을 가지고 있다라고 한다. 데이터가 맞긴 맞지만, 너무 커다란 변동성을 가지게 되면서, 너무 약한 일관성?을 가지게 된다.
3. 중간 건 그냥 잘 맞는다고 함, Just right!

1. 로지스틱 리그레션에서도 이와같은 과소적합과 과대적합의 예를 찾을 수 있다.
2. 적절하게 디시전 바운더리가 형성될 수 있디만, 피쳐가 많아지면, 오버피팅 되어, 높은 분산을 가지게 되어 버린다.

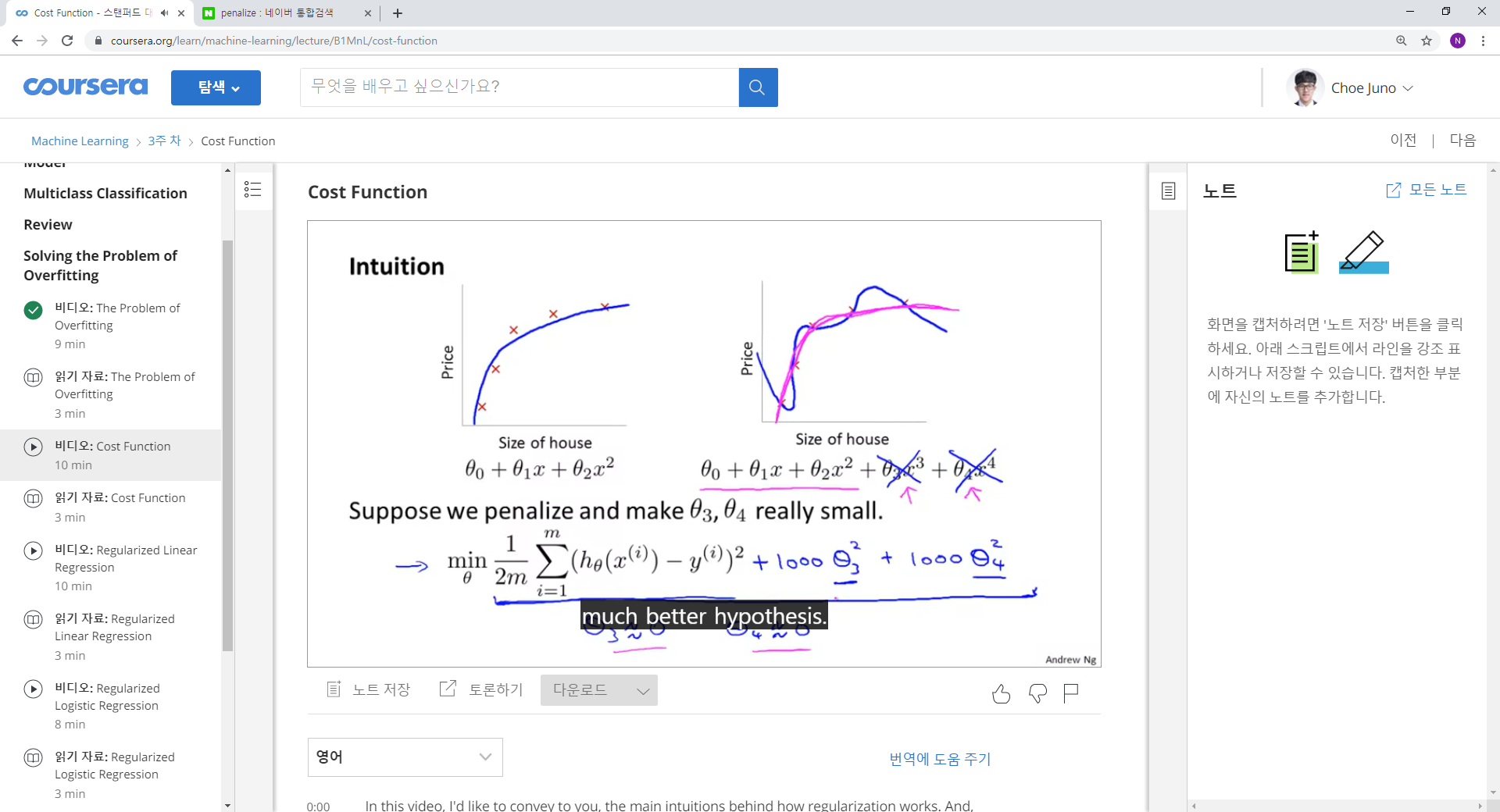
1. 어떻게 이것이 과적합인지 알 수 있을까?
2. 집값을 예측하는데 트것ㅇ이 너무 많고, 그 많은 특성들이 예측에 도움이 될 것 같을 떄? 어떻게 해야 할까?

1. 문제 해결에는 두 가지 방법이 있다. 첫 째는 피쳐를 직접 선택하는 방법 그리고 모델을 선택하는 방법이 ㅣㅆ다.
2. 두번 째는 정규화 방법이다. 모든 특성들을 남기되, 영향 규모를 줄여주는 것이다. 즉 세타 값을 줄이는 것이다. 특성을 버리기 싫으니 영향력을 줄이는 것이다.
B. Cost function
*penalize 처벌하다, 벌칙을 과하다
1
... 중간에 삭제됨
다항식의 비용함수를 정규화 시키기 위해서, 세타 값이 0에 근사하도록 한다. 그렇기 위해서, 비용함수를 계산할 때. 람다와 모든 세타의 합의 곱을 더해 주게 되는데, 이때 람다는 정확한 모델을 만드는 것과,세타를 0에 근사하게 하는 두 힘의 작용에서 조절하는 역할을 하게 된다.

1. 로지스틱 회귀 함수에서도 또한 같다. 로지스틱 회귀에서는 가설 h가 -log()형태를 가지게 된다 그렇기 때문에 위와 같은 비용함수의 형태를 보였다.
2. 여기서도 똑같이 그 합을 더해 주는 형태로 최솟값을 구할 수 있다.

1. 선형회귀의 비용함수에 취해줬던 것처럼 람다와 세타의 곱을 m으로 나눠준 값을 더해주게 된다.
2. 다시 한번 말하지면, 형식이 같다고 해서 같은 비용함수 공식이 아니다. 이미 가설 h를 설정하는 방법에서 부터 차이를 보이기 떄문이다.

1. 경사 하강법보다 더 진보된 형태의 최적화 방법이 fminunc라는 방법이고이 또한 경사하강법과 같은 형태로 세타에 대해서 동시에 업데이트를 하며 최적의 세타값을 찾아가게 된다.
2. 결국 우리는 비선형적인 분류 방법을 찾고자 이러한 다항식을 만들고, 다항식을 정규화 하는 것을 배워야 했던 것이다. 어떤 분류나 예측이 선형적이라면, 그것은 쉽게 계산 가능하며, 예측 가능하다는 것이지만, 그렇지 못한 부분에 대하여 우리는 지금은, 머신러닝을 통해 적절히 예측할 수 있게 되는 것이다.
'2019년 혁신성장 청년인재 집중양성(빅데이터) > [COURSERA] Machine Learning Stanford Uni' 카테고리의 다른 글
| [week4] Neural Network (0) | 2019.09.30 |
|---|---|
| [week4] Non-linear Hypotheses, Motivation (0) | 2019.09.30 |
| [week3] Multiclass Classification (0) | 2019.09.26 |
| [week3] Classification and Representation (0) | 2019.09.24 |
| [week2] vectorization (0) | 2019.09.14 |



