A. Problem Motivation

1. 분포의 밀도를 이용하여, 분포의 중심에서 멀어진 값을 이상치로 분류하는 것이다. 통계적접근법.

1. 이상치 검색의 예시 : 어떤 관찰 값이 사기일 확률, 제조 공정에서의 불량품 검색, 데이터 센타에서의 컴퓨터 감독
B. Gaussuan Distribution

1. 가우시안 분포에서의 확률은 면적으로 표현되며, 그 공식은 위와 같다. 가우시간 분포는 평균값인 뮤와 표준편차인 시그마의 제곱으로 표현될 수 있다.
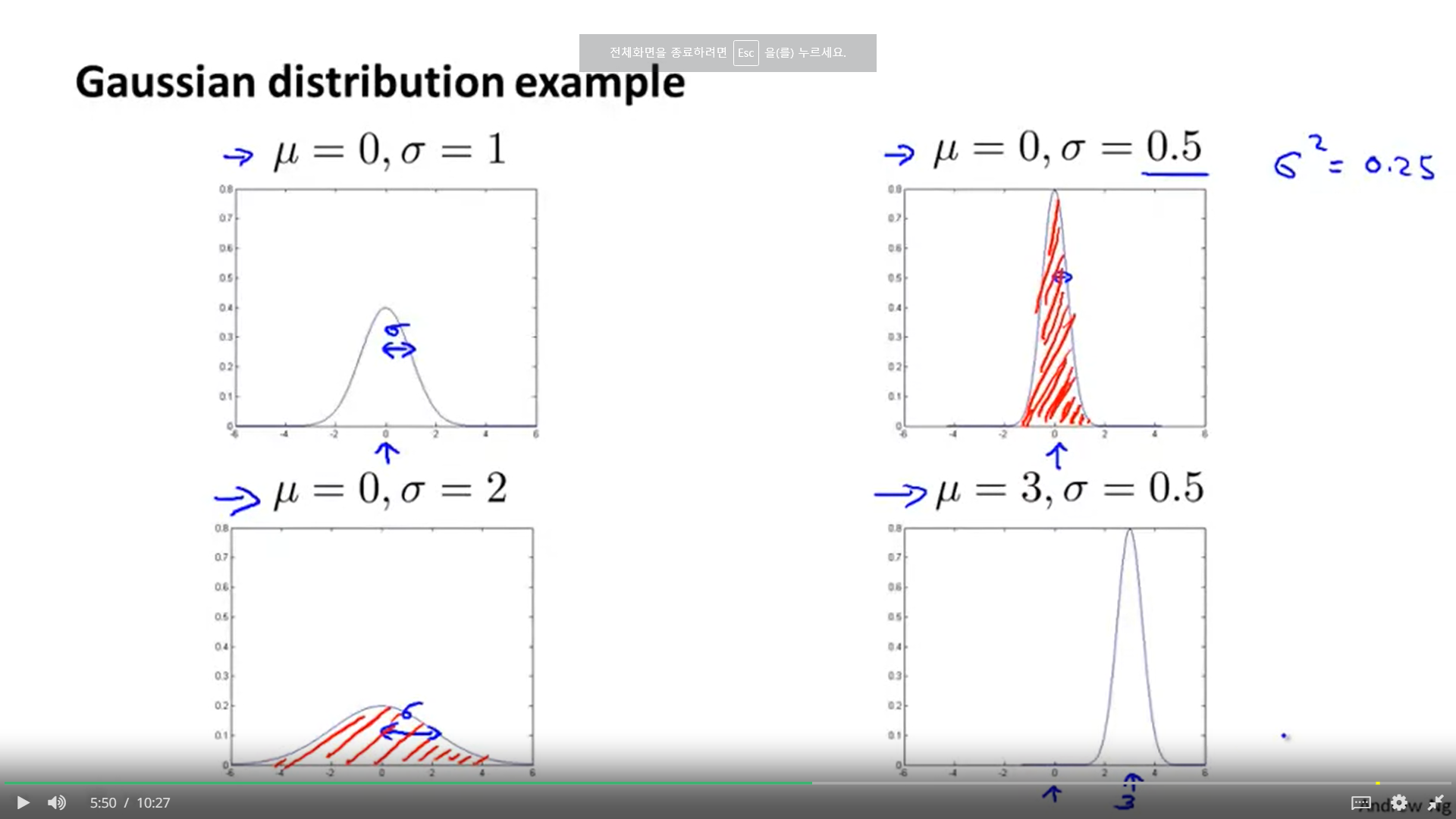
1. 간단하다. 뮤는 중앙의 데이터가 가장 많은 지점, 표준편차 시그마가 커질수록 넓게 펴진다.
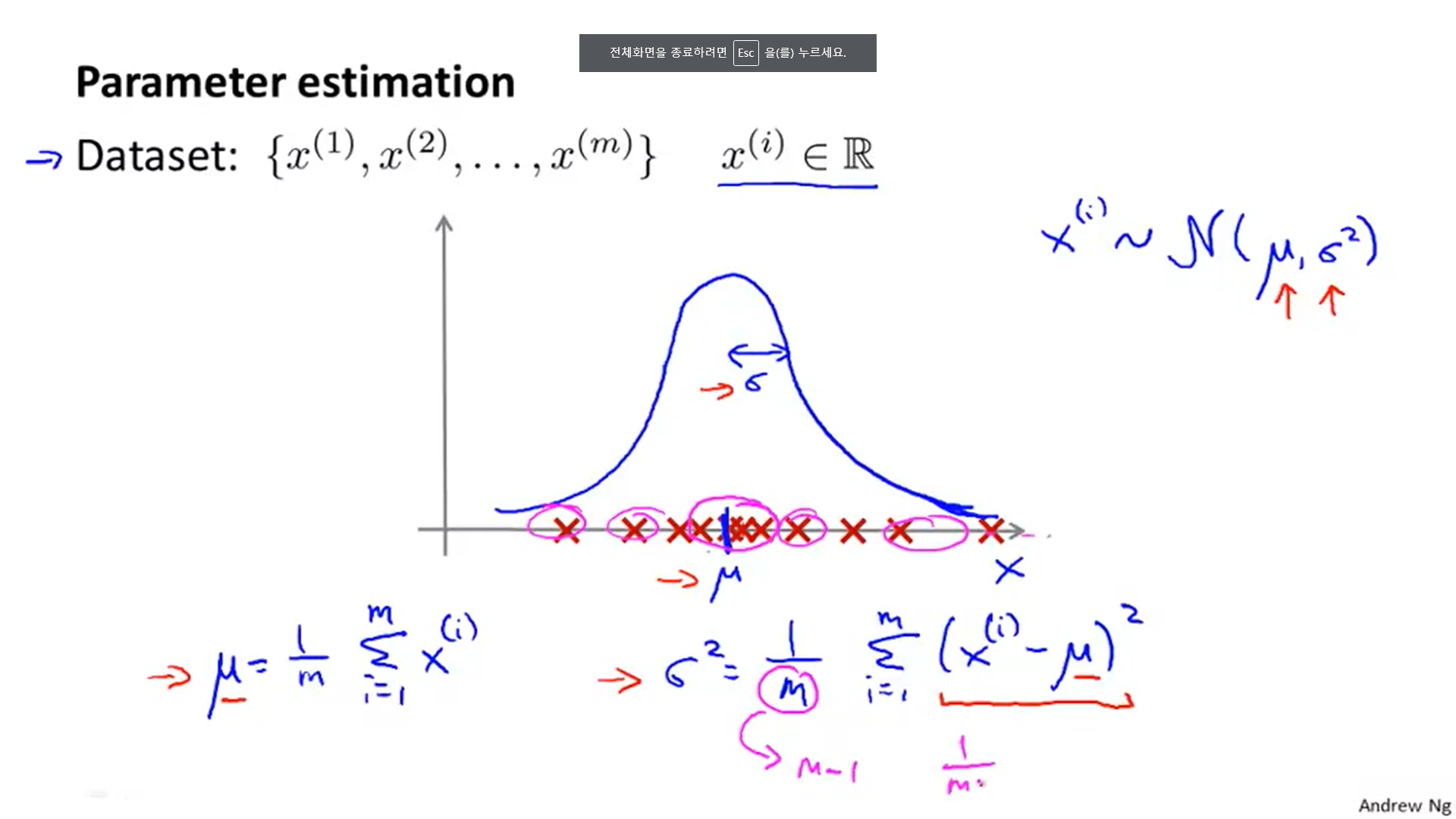
1. 뮤 말그대로 평균이기 때문에 m으로 나눠주는 것이고, 시그마의 제곱은 분산이기 때문에 중앙에서 멀어진 정도의 평균을 재는 것에 사용된다.
C. Algorithm

1. 알고리즘 역시 간단하다. 각 피쳐의 분포로부터, 그 피쳐가 나올 확률을 모두 곱하는 것이다.
2. 교수님께서 친절하게 웃기게 생긴 파이에 대해서 이야기 해주셨다. 우리가 알고 있는 시그마는 모든 값을 더하는 것이지만, 저 파이는 값을 곱하는 것을 줄여쓰는 기호라고 한다.

1. 첫째, 피쳐를 선택한다.
2. 둘째, 각 피쳐들의 분포의 특성인 뮤와 시그마를 구한다.
3. 셋째, 확률을 계산한다
4. 넷째, 그 확률이 엡실론보다 작다면 이것은 이상한 것이다.
'2019년 혁신성장 청년인재 집중양성(빅데이터) > [COURSERA] Machine Learning Stanford Uni' 카테고리의 다른 글
| [week9] Predicting Movie Rating (0) | 2019.11.07 |
|---|---|
| [week9] Building an Anomaly Detection System (0) | 2019.11.07 |
| [week8] Applying PCA (0) | 2019.11.03 |
| [week8] Principal Component Analysis (0) | 2019.11.03 |
| [week8] Data Compression (0) | 2019.11.03 |



