
1. Tree는 나무처럼 생긴 데이터의 구조이다. 트리는 뿌리(root)라는 장소로부터 출발하여 가지(branches)라고 불리는 데이터를 더해간다. 나무처럼, 데이터는 많은 방향으로 뻗쳐나간다.
2. Tree는 Linked List의 확장판이다. 이전 원소가 다음원소를 가리키는 Linked List와 달리, Tree는 이전 원소가 여러개의 원소를 가리킬 수 있다. Linked List는 수평적이지만, Tree는 수직적이다.


1. Trees의 모든 원소는 연결되어 있으며, 순환하는 고리를 형성하지 않는다.

1. 얼마나 많은 연결을 가져야 루트에 도달할 수 있는지에 더하기 일을 한 것이 노드의 레벨이다. 트리의 노드는 부모-자식관계를 가지는 것으로 묘사된다.
2.낮은 레벨에 있는 노드를 부모라고 부르며, 높은레벨에 있는 노드를 자식이라고 부른다. 중간 단계에 있는 노드는 부모/자식 노드가 동시에 될 수 있다.
3. 일반적인 부모관계랑 다른 것은 자식 노드는 단 하나의 부모 노드를 갖는다는 것이다. 같은 부모 노드에서 나온 자식 노는 자매관계(sibling)이라고 부른다.
4. 트리의 맨 끝에 위치하여 자식노드가 없는 자식노드를 external node 혹은 잎(leaves)라고 부른다. 그와 반대로 부모 노드는 Internal node라고 부른다. 노드 사이의 연결을 edge라고 부를 수 있으며, edge들의 집합을 path라고 부른다.
5.노드의 높이는 가장 먼 잎으로 부터의 edge의 수다.그렇기에 잎의 높이는 0이다. 트리의 높이는 뿌리 노드의 높이와 같다. 그와 반대로 노드의 깊이는 루트 노드 까지의 edfe의 수다.

1. 트리 구조의 데이터를 가로지르는 방법은 딱 정해져 있지 않다.
2. DFS는 Depth First Search다. 뿌리 노드에서 출발하여 잎 노드까지 찍고 다른 곳으로 이동한다. DFS의 철학은 자식이 있다면 그 자식을 우선해서 확인한다! 이다.
3. BFS는 Breadth first search다. BFS의 철학은 같은 레벨에 있는 노드를 우선적으로 살핀다이다.

1.DFS도 방법이 나눠진다. 첫째가 Pre-Order다. 직관적으로 생각하는 것이 Pre-Order다 지나가면서 다 훍는다.

1. In Order인 이유는 잘보면 레알 왼쪽에서 오른쪽으로 차례대로 훍으면서 가기 때문이다.

1. 일단 서브 트리 내에서는 깊이가 우선이 되어서 파악하는 것이 Post-order이다.

1. 바이너리 트리는 자식 노드를 0,1,2개 가질 수 있는 트리다.
2. 트리를 탐색할 경우 위에서 보았던 탐색 알고리즘을 쓰면 된다.
3. 트리의 노드를 삭제하고 싶다면 몇 가지를 생각해야 한다. 인터널 노드를 삭제하면, 트리에 갭이 생겨버린다. 이때는 하나의 자식 노드를 부모노드를 격상할 수 있다. 아니면 상위 노드와 연결하는 방법이 있다.
1. 삽입 시에는 최대 2가지의 자식 노드만을 가질 수 있다는 룰만 지켜주면 된다. 그렇다면 오픈된 노드를 찾아야 하는데 운이 좋지 않으면 트리의 높이만큼 움직여야 한다.
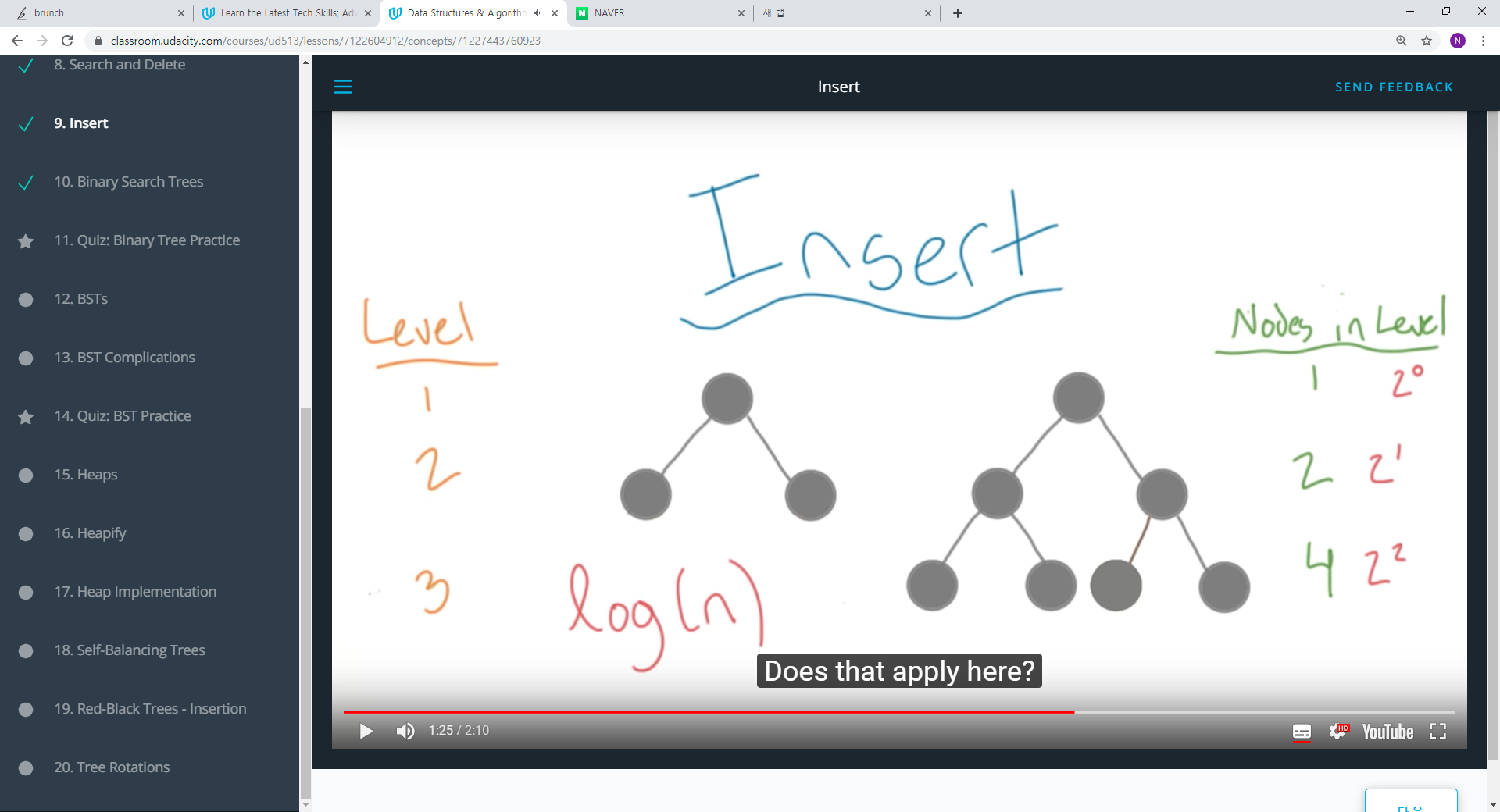
1. 레벨이 높아지는 만큼 2의 제곱승으로 자식노드의 수는 많아진다.
2. 트리는 선천적으로 잘 정리 되어 있지 않다. 트리를 보면 전체 구조는 알 수 있지만, 어떤 원소가 어디에 위치 하는 지는 모른다.

1. 좀더 자세한 타입의 바이너리 트리를 바이너리 서치 트리 BST라고 부른다.
2. BST는 정렬되어 있기 때문에 모든 값은 왼쪽에서 시작되어서 오른쪽으로 갈수록 커진다.
3. 정렬되어 있기 때문에 모든 원소를 찾아보지 않아도 된다.

1. 이것 역시 바이너리 트리다. 하지만 언벨런스하다고 할 수 있다. 언벨런스 노드는 노드가 한 쪽으로 치우쳐져 있다. 이럴 경우가 서치를 하는 딜리트를 하든 최악이다. 꼼수를 부릴 수 없기 때문에 시간은 항상 선형적으로 걸린다.즉 모든 원소를 다 봐야 한다는 뜻이다. 좋을 때는 O(log(n))이지만 안 좋을 때는 O(n)이 걸린다.

1. 힙은 부가적인 규칙을 가지고 있는 트리의 타입 중 하나다.
2. 힙에서 원소는 증가하거나 감소하는 순서를 갖는다, 즉 루트는 최대이거나 최소다.
3. 맥스힙에서는 부모는 자식보다 항상 큰 값을 가지며, 루트는 최대 값을 가진다.
4. 그 반대가 민힙이다.
5. 힙은 바이너리 트리일 필요가 없기 때문에 여러 개의 자식 노드를 가질 수 있다.
6. 바이너리 힙은 반드시 "complete"해야 한다. Complete하다는 것은 마지막 하나를 제외한 모든 노드가 2개의 자식 노를 가지고 있어야 한다는 의미다. 이 경우에 최대 값을 꼭지점(peak)이라고도 부른다.

1. 노드를 삽입할 때, 삽입되는 노드가 부모노드보다 크다면 heapify를 해야한다. heapify는 힙의 특성에 기반하여 트리의 순서를 정렬하는 것을 말한다.

1. 루트 노드가 삭제 되었다고 하더라도, Heapify를 통해 재정렬을 할 수 있다.

1. heap에서 최악의 경우 O(log(n))의 시간적 비용이 든다.

1. 힙은 자주 배열형태로 저장된다.

1. 배열에 데이터를 저장하는 것은 공간을 아껴준다.
2. 어레이는 포인터를 지정할 필요가 없기 때문에 그만큼 공간을 줄여준다.

1. 밸런스드 트리는 노드가 적은 레벨에 밀집되어 있지만, 언벨런스드 트리는 노드가 많은 레벨에 산개되어 있다.
2. 최악이 언벨런스드 트리가 링크드 리스트와 같을 때이다.
3. 셀프 벨런싱 트리는 레벨의 사용을 최소화하는 트리다.
4. 삽입과 삭제에 추가적인 알고리즘을 사용하여 레벨의 사용을 최소화한다.

1. 두 가지 타입의 노드가 있다.
2. null이 리프 형태로 존재한다. 2개의 리프를 가지고 있지 않은 모든 노드는 null 을 갖는다. 그리고 null은 검정색이다.
3. 노드가 빨강색이라면 자식 노드는 검정색이다.
4. 루트 노드는 검정색이다.
5. null 노드로 향하는 모든 path는 모두 같은 수의 검정색 노드를 포함한다.